'linalg' Dialect

[TOC]

Rationale

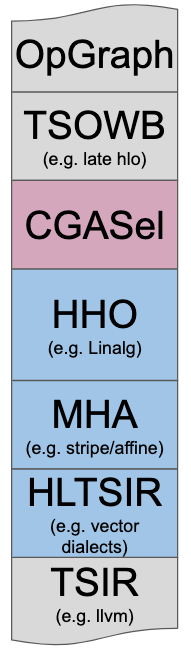
Linalg is designed to solve the High-level Hierarchical Optimization (HHO box) in MLIR and to interoperate nicely within a Mixture Of Expert Compilers environment (i.e. the CGSel box).

The Rationale Document goes into significantly more design and architectural decision details.

Set of Key Transformations

The following key transformations have been central to driving the design of Linalg. They are all implemented in terms of the properties of the linalg.generic OpInterface and avoid the pitfall of relying on hardcoded one-off op knowledge.

The textual form description of these transformations is left for future work. Still, it is useful to at least the key transformations that are performed on the Linalg IR and that have influenced its design:

1. Progressive Buffer Allocation.
2. Parametric Tiling.
3. Promotion to Temporary Buffer in Fast Memory.
4. Tiled Producer-Consumer Fusion with Parametric Tile-And-Fuse.
5. Map to Parallel and Reduction Loops and Hardware.
6. Vectorization: Rewrite in Vector Form.
7. Lower to Loops (Affine, Generic, and Parallel).
8. Lower to Library Calls or Special Instructions, Intrinsics or ISA.
9. Partially Lower to Iterations Over a Finer-Grained Linalg Op.

High-Level Description of Linalg Ops

Linalg takes at least some inspiration from all previously listed prior art. The design enables the definition of CustomOps with generic properties that enable key transformations, including lowering to scalar load/store and other operations or to external library calls and intrinsics.

These ops can have either tensor or buffer operands, subject to conventions and limitations.

Payload-Carrying Ops

Linalg defines two payload carrying operations that implement the structured ops abstraction on tensors and buffers. This is architected as two generic operations linalg.generic (resp. linalg.indexed_generic) that can express custom operations with index-free semantics (resp. indexing semantics). The properties of these generic ops are the result of applying the guiding principles described in the Rationale Document. They are listed next, with a brief example and discussion for each.

Property 1: Input and Output Operands Define The Iteration Space

A linalg.generic op fully derives the specification of its iteration space from its operands. The property enforces that a localized IR element (the op) has all the information needed to synthesize the control-flow required to iterate over its operands, according to their type. This notion of IR localization bears some resemblance to URUK.

Consider the following fully specified linalg.generic example. Here, the first operand is a memref of f32 scalar elements that has an ordinary identity layout, and the second one is a memref of 4-element vectors with a 2-strided, 1-offset layout.

// File name: example1.mlir
#accesses = [
  affine_map<(m) -> (m)>,
  affine_map<(m) -> (m)>
]
#attrs = {
  args_in = 1,
  args_out = 1,
  indexing_maps = #accesses,
  iterator_types = ["parallel"]
}
// memory layouts
#identity = affine_map<(d0) -> (d0)>

func @example(%A: memref<?xf32, #identity>,
              %B: memref<?xvector<4xf32>, offset: 1, strides: [2]>) {
  linalg.generic #attrs %A, %B {
  ^bb0(%a: f32, %b: vector<4xf32>):
    %c = "some_compute"(%a, %b): (f32, vector<4xf32>) -> (vector<4xf32>)
    linalg.yield %c: vector<4xf32>
  } : memref<?xf32, #identity>, memref<?xvector<4xf32>, offset: 1, strides: [2]>
  return
}

The property "Input and Output Operands Define The Iteration Space" is materialized by a lowering into a form that will resemble:

// Run: mlir-opt example1.mlir -allow-unregistered-dialect -convert-linalg-to-loops
// This converted representation is in the `scf` dialect.
// It's syntax can be found here: https://mlir.llvm.org/docs/Dialects/SCFDialect/
#map0 = affine_map<(d0) -> (d0 * 2 + 1)>

func @example(%arg0: memref<?xf32>, %arg1: memref<?xvector<4xf32>, #map0>) {
  %c0 = constant 0 : index
  %c1 = constant 1 : index
  %0 = dim %arg0, %c0 : memref<?xf32>
  scf.for %arg2 = %c0 to %0 step %c1 {
    %1 = load %arg0[%arg2] : memref<?xf32>
    %2 = load %arg1[%arg2] : memref<?xvector<4xf32>, #map0>
    %3 = "some_compute"(%1, %2) : (f32, vector<4xf32>) -> vector<4xf32>
    store %3, %arg1[%arg2] : memref<?xvector<4xf32>, #map0>
  }
  return
}

The property participates in simplifying analyses and transformations. For instance, it guarantees no out-of bounds access can occur by construction (assuming dynamic operand dimensions agree with each other, which is the purpose of the assert runtime check).

Before lowering to loop form, loop induction variables and iterators are not yet materialized. This is a necessary property if we want an abstraction that works on both tensor values and buffers because values don’t escape loops/nesting.

The main implications are that:

1. The semantics of the ops are restricted to operate on structured data types, on which we can define an iterator.
2. This does not model arbitrary code with side-effects.

We do not think these are serious limitations in practice because MLIR is all about mixing different levels of abstractions in the same IR. As long as Linalg can progressively lower to the next level of abstraction, it can also be just bypassed for things that do not fit.

At the same time, conditioning op semantics on structured data types is a very promising path towards extensibility to non-dense tensors as experience with LIFT abstractions for sparse and position-dependent arrays, as well as TACO, has shown.

Property 2: Reversible Mappings Between Control and Data Structures

A linalg.generic defines the mapping between the iteration space (i.e. the loops) and the data.

Consider the following fully specified linalg.generic example. Here, the first memref is a 2-strided one on both of its dimensions, and the second memref uses an identity layout.

// File name: example2.mlir
#indexing_maps = [
  affine_map<(i, j) -> (j, i)>,
  affine_map<(i, j) -> (j)>
]
#attrs = {
  args_in = 1,
  args_out = 1,
  indexing_maps = #indexing_maps,
  iterator_types = ["parallel", "parallel"]
}

func @example(%A: memref<8x?xf32, offset: 0, strides: [2, 2]>,
              %B: memref<?xvector<4xf32>>) {
  linalg.generic #attrs %A, %B {
  ^bb0(%a: f32, %b: vector<4xf32>):
    %c = "some_compute"(%a, %b): (f32, vector<4xf32>) -> (vector<4xf32>)
    linalg.yield %c: vector<4xf32>
  }: memref<8x?xf32 , offset: 0, strides: [2, 2]>, memref<?xvector<4xf32>>
  return
}

The property "Reversible Mappings Between Control and Data Structures" is materialized by a lowering into a form that will resemble:

// Run: mlir-opt example2.mlir -allow-unregistered-dialect -convert-linalg-to-loops
#map0 = affine_map<(d0, d1) -> (d0 * 2 + d1 * 2)>

func @example(%arg0: memref<8x?xf32, #map0>, %arg1: memref<?xvector<4xf32>>) {
  %c8 = constant 8 : index
  %c0 = constant 0 : index
  %c1 = constant 1 : index
  %0 = dim %arg0, %c1 : memref<8x?xf32, #map0>
  scf.for %arg2 = %c0 to %0 step %c1 {
    scf.for %arg3 = %c0 to %c8 step %c1 {
      %1 = load %arg0[%arg3, %arg2] : memref<8x?xf32, #map0>
      %2 = load %arg1[%arg3] : memref<?xvector<4xf32>>
      %3 = "some_compute"(%1, %2) : (f32, vector<4xf32>) -> vector<4xf32>
      store %3, %arg1[%arg3] : memref<?xvector<4xf32>>
    }
  }
  return
}

This mapping needs to be reversible because we want to be able to go back and forth between the two and answer questions such as:

• Given a subset of the iteration space, what subset of data does it read and write?
• Given a subset of data read or written, what subset of the iteration space is responsible for this read or write?

Answering these 2 questions is one of the main analyses that Linalg uses to implement transformations such as tiling, tiled producer-consumer fusion, and promotion to temporary buffers in fast memory.

In the current implementation, linalg.generic uses a list of AffineMaps (see the #indexing_maps attribute in the previous examples). This is a pragmatic short-term solution, but in the longer term note that this property could be even evaluated dynamically, similarly to inspector-executor algorithms.

Property 3: The Type Of Iterators is Defined Explicitly

A linalg.generic op fully declares the type of its iterators. This information is used in transformations.

These properties are derived from established practice in the field and mirror the properties from Ken Kennedy's Optimizing Compilers for Modern Architectures. The key idea of legality of loop transformations expressed by Kennedy is that the lexicographic order of all dependence vectors must be preserved.

This can be better captured directly at the loop level thanks to specific iterator types, among which: parallel, reduction, partition, permutable/monotonic, sequential, dependence distance, ...

These types are traditionally the result of complex dependence analyses and have been referred to as "bands" in the polyhedral community (e.g. parallel bands, permutable bands, etc, in ISL schedule tree parlance).

Specifying the information declaratively in a linalg.generic allows conveying properties that may be hard (or even impossible) to derive from lower-level information. These properties can be brought all the way to the moment when they are useful for transformations, used and then discarded.

Additionally, these properties may also be viewed as a contract that the frontend/user guarantees and that the compiler may take advantage of. The common example is the use of data-dependent reduction semantics for specifying histogram computations. If the frontend has additional knowledge that proper atomic operations are available, it may be better to specify parallel semantics and use the special atomic in the computation region.

At this time, Linalg only has an explicit use for parallel and reduction loops but previous experience shows that the abstraction generalizes.

Property 4: The Compute Payload is Specified With a Region

A linalg.generic op has a compute payload that is fully generic thanks to the use of Regions.

The region takes as arguments the scalar elemental types of the tensor or buffer operands of the linalg.generic. For flexibility and ability to match library calls, additional special values may be passed. For instance, a linalg.fill operation takes a buffer and an additional scalar value.

At this time there are no additional restrictions to the region semantics. This is meant to allow the exploration of various design tradeoffs at the intersection of regions and iterator types. In particular, the frontend is responsible for the semantics of iterator types to correspond to the operations inside the region: the region can capture buffers arbitrarily and write into them. If this conflicts with some parallel iterator requirement, this is undefined behavior.

Previous examples already elaborate compute payloads with an unregistered function "some_compute". The following code snippet shows what the result will be when using a concrete operation addf:

// File name: example3.mlir
#indexing_maps = [
  affine_map<(i, j) -> (i, j)>,
  affine_map<(i, j) -> (i, j)>,
  affine_map<(i, j) -> (i, j)>
]
#attrs = {
  args_in = 2,
  args_out = 1,
  indexing_maps = #indexing_maps,
  iterator_types = ["parallel", "parallel"]
}
func @example(%A: memref<?x?xf32>, %B: memref<?x?xf32>, %C: memref<?x?xf32>) {
  linalg.generic #attrs %A, %B, %C {
  ^bb0(%a: f32, %b: f32, %c: f32):
    %d = addf %a, %b : f32
    linalg.yield %d : f32
  }: memref<?x?xf32>, memref<?x?xf32>, memref<?x?xf32>
  return
}

This function basically element-wise adds up two matrices (%A and %B) and stores the result into another one (%C).

The property "The Compute Payload is Specified With a Region" is materialized by a lowering into a form that will resemble:

// Run: mlir-opt example3.mlir -convert-linalg-to-loops
#indexing_maps = [
  affine_map<(i, j) -> (i, j)>,
  affine_map<(i, j) -> (i, j)>,
  affine_map<(i, j) -> (i, j)>
]
#attrs = {
  args_in = 2,
  args_out = 1,
  indexing_maps = #indexing_maps,
  iterator_types = ["parallel", "parallel"]
}
func @example(%A: memref<?x?xf32>, %B: memref<?x?xf32>, %C: memref<?x?xf32>) {
  linalg.generic #attrs %A, %B, %C {
  ^bb0(%a: f32, %b: f32, %c: f32):
    %d = addf %a, %b : f32
    linalg.yield %d : f32
  }: memref<?x?xf32>, memref<?x?xf32>, memref<?x?xf32>
  return
}

In the process of lowering to loops and lower-level constructs, similar requirements are encountered, as are discussed in the inlined call op proposal. We expect to be able to reuse the common lower-level infrastructure provided it evolves to support both region arguments and captures.

Property 5: May Map To an External Library Call

A linalg.generic op may map to an external library call by specifying a SymbolAttr. At this level of abstraction, the important glue is the ability to perform transformations that preserve the structure necessary to call the external library after different transformations have been applied.

This involves considerations related to preservation of op semantics and integration at the ABI level. Regardless of whether one wants to use external library calls or a custom ISA, the problem for codegen is similar: preservation of a fixed granularity.

Consider the following example that adds an additional attribute library_call="pointwise_add" that specifies the name of an external library call we intend to use:

// File name: example4.mlir
#indexing_maps = [
  affine_map<(i, j) -> (i, j)>,
  affine_map<(i, j) -> (i, j)>,
  affine_map<(i, j) -> (i, j)>
]
#attrs = {
  args_in = 2,
  args_out = 1,
  indexing_maps = #indexing_maps,
  iterator_types = ["parallel", "parallel"],
  library_call = "pointwise_add"
}
func @example(%A: memref<?x?xf32>, %B: memref<?x?xf32>, %C: memref<?x?xf32>) {
  linalg.generic #attrs %A, %B, %C {
  ^bb0(%a: f32, %b: f32, %c: f32):
    %d = addf %a, %b : f32
    linalg.yield %d : f32
  }: memref<?x?xf32>, memref<?x?xf32>, memref<?x?xf32>
  return
}

The property "Map To an External Library Call" is materialized by a lowering into a form that will resemble:

// Run: mlir-opt example4.mlir -convert-linalg-to-std
// Note that we lower the Linalg dialect directly to the Standard dialect.
// See this doc: https://mlir.llvm.org/docs/Dialects/Standard/

#map0 = affine_map<(d0, d1)[s0, s1, s2] -> (d0 * s1 + s0 + d1 * s2)>

func @example(%arg0: memref<?x?xf32>, %arg1: memref<?x?xf32>, %arg2: memref<?x?xf32>) {
  %0 = memref_cast %arg0 : memref<?x?xf32> to memref<?x?xf32, #map0>
  %1 = memref_cast %arg1 : memref<?x?xf32> to memref<?x?xf32, #map0>
  %2 = memref_cast %arg2 : memref<?x?xf32> to memref<?x?xf32, #map0>
  call @pointwise_add(%0, %1, %2) : (memref<?x?xf32, #map0>, memref<?x?xf32, #map0>, memref<?x?xf32, #map0>) -> ()
  return
}
func @pointwise_add(memref<?x?xf32, #map0>, memref<?x?xf32, #map0>, memref<?x?xf32, #map0>) attributes {llvm.emit_c_interface}

Which, after lowering to LLVM resembles:

// Run: mlir-opt example4.mlir -convert-linalg-to-std | mlir-opt -convert-std-to-llvm
// Some generated code are omitted here.
func @example(%arg0: !llvm<"float*">, ...) {
  ...
  llvm.call @pointwise_add(...) : (!llvm<"float*">, ...) -> ()
  return
}

llvm.func @pointwise_add(%arg0: !llvm<"float*">, ...) attributes {llvm.emit_c_interface} {
  ...
  llvm.call @_mlir_ciface_pointwise_add(%9, %19, %29) : (!llvm<"{ float*, float*, i64, [2 x i64], [2 x i64] }*">, !llvm<"{ float*, float*, i64, [2 x i64], [2 x i64] }*">, !llvm<"{ float*, float*, i64, [2 x i64], [2 x i64] }
*">) -> ()
  llvm.return
}
llvm.func @_mlir_ciface_pointwise_add(!llvm<"{ float*, float*, i64, [2 x i64], [2 x i64] }*">, !llvm<"{ float*, float*, i64, [2 x i64], [2 x i64] }*">, !llvm<"{ float*, float*, i64, [2 x i64], [2 x i64] }*">) attributes {llvm.emit_c_interface}

Convention For External Library Interoperability

The linalg dialect adopts a convention that is similar to BLAS when offloading operations to fast library implementations: pass a non-owning pointer to input and output data with additional metadata. This convention is also found in libraries such as MKL, OpenBLAS, BLIS, cuBLAS, cuDNN, etc.. and more generally at interface points across language boundaries (e.g. C++ / Python).

Generally, linalg passes non-owning pointers to View data structures to pre-compiled library calls linked externally.

There is an ongoing discussion on the topic of extending interoperability in the presence of key attributes.

Property 6: Perfectly Nested Writes To The Whole Output Operands

Perfectly nested loops form a particularly important class of structure that enables key loop transformations such as tiling and mapping to library calls. Unfortunately, this type of structure is easily broken by transformations such as partial loop fusion. Tiling and mapping to library calls become more challenging, or even infeasible. Linalg ops adopt perfect-nestedness as a first-class property: the structure cannot be broken and is transported in the IR by construction.

A linalg.generic op represents a perfectly nested loop nest that writes the entire memory region. This is a structural constraint across regions and loops that has proven to be key in simplifying transformations.

One particular point to mention is that converting imperfectly nested code into perfectly nested code can often be done with enough loop distribution and embedding of conditionals down to the innermost loop level.

Previous experience with Tensor Comprehensions gave us the intuition that forcing innermost control-flow nesting is a lot like writing data-parallel code with arrays of boolean values and predication. This type of trick has also been used before in polyhedral compilers to convert non-affine control into affine compute dependencies.

While it may be possible to automate such rewrites from generic IR, linalg.generic just forces the semantics for now.

The key implication is that this conversion to deep predication needs to be undone once we are done with Linalg transformations. After iterators and induction variables are materialized (i.e. after lowering out of linalg.generic occurred), the overall performance will be greatly influenced by the quality of canonicalizations, foldings and Loop Independent Code Motion (LICM).

In the grander scheme, the reliance on late LICM was deemed a necessary risk.

Putting it Together

As it stands, the six properties above define the semantics of a linalg.generic op. It is an open question whether all of these semantics are strictly necessary in practice and whether some should or could be derived automatically while still maintaining the core guiding principles.

For the time being, we have settled on the combination of these properties because of empirical evidence building and working on multiple high-level compilers. As we lay those down and engage more with the community, we expect multiple rounds of discussions and design changes to the original architecture.

Tensors and Buffers: Conventions and Limitations

Tensors are immutable SSA values, buffers are mutable regions of memory subject to side-effects and aliasing. As a consequence, output buffers are passed as operands whereas output tensors are new SSA values corresponding to op results. Inputs can be arbitrary tensors or buffers and are always passed as operands.

The following convention is currently in-flight and is in the process of replacing other existing conventions. The following convention currently applies to "named" structured ops which are auto-generated by the linalg-ods tool.

The convention adopted is as follows:

1. A first block of ins op operands hold read-only inputs of ShapedType.
2. An optional second block of outs op operands hold read-write output buffers of MemRefType.
3. An optional third block of init operands hold initialization tensors of RankedTensorType. Such tensors can appear when the op performs a reduction and returns a tensor.

Structured ops with fully parallel semantics, have empty init. They may either write in-place into outs buffers or return new tensors.

Structured ops with reduction semantics and output tensor(s) however have additional restrictions:

1. They can only return a single tensor for now.
2. They cannot have any output buffer operand (i.e. outs is empty).
3. They have exactly one init tensor of the same type as the unique output tensor. Such an init tensor does not have an explicit associate indexing map. Instead the map of the result tensor is used to signify that the init and the result are "tied".

Points 1. and 2. keep complexity of the representation in check by allowing only a single result tensor, when reductions are present.

Point 3. is related to the fact that SSA values cannot represent in-place updates. Instead, linalg adopts a similar convention that exists in e.g. vector.outerproduct: the value that is reduced into is passed as an explicit argument and a new result of the same shape is produced.

It is expected buffer allocation will fold this last input onto the result in a single output buffer argument, which is why the same indexing map is required: the last input operand is said to be "tied" to the result.

Alternative, more complex representations, would allow for:

1. Multiple results and init tensors in arbitrary orders, which could be captured by an extra ArrayAttr of position pairs.
2. Relaxing the conditions on the indexing map equalities on the each pair and e.g. allow implicit broadcasts of the input.

These representations are deemed unnecessarily complex for now and are left for future discussion.

As an illustration, the syntax for a linalg.matmul writing into a buffer is:

linalg.matmul ins(%a, %b : memref<?x?xf32>, tensor<?x?xf32>)
             outs(%c : memref<?x?xf32>)

, whereas the syntax for a linalg.matmul returning a new tensor is:

%d = linalg.matmul ins(%a, %b : tensor<?x?xf32>, memref<?x?xf32>)
                  init(%c : tensor<?x?xf32>)
                    -> tensor<?x?xf32>

Data Representation: Views

The current implementation uses the Strided MemRef (a.k.a View) abstraction. The name View is used interchangeably in linalg to signify Strided MemRef. In the future we expect to use other structured data types and support ragged, mixed-sparse and other types. We expect to draw on the experience from existing LIFT abstractions for sparse and position-dependent arrays.

Metadata Ops

A set of ops that manipulate metadata but do not move memory. These ops take view operands + extra attributes and return new views. The returned views generally alias the operand view. At the moment the existing ops are:

* `std.view`,
* `std.subview`,
* `linalg.range`,
* `linalg.slice`,
* `linalg.transpose`.
* `linalg.reshape`,

Future ops are added on a per-need basis but should include:

* `linalg.tile`,
* `linalg.intersection`,
* `linalg.convex_union`,
* `linalg.difference` (would need to work on a list of views).

These additional operations correspond to abstractions that have been known to work in the field of large-scale distributed stencil computations.

In a longer-term future, the abstractions from Legion data-centric programming model seem generally appealing.

Named Payload-Carrying Ops

Additionally, linalg provides a small subset of commonly named operations:

* `linalg.copy`,
* `linalg.fill`,
* `linalg.dot`,
* `linalg.matmul`,
* `linalg.conv`.

These named operations adhere to the linalg.generic op interface. Work is in progress to define declarative mechanisms to automatically generate named ops from a description in terms of only the generic op interface.

This is the main reason there are only a small number of ops today: we expect them to be auto-generated from Tablegen soon.

Named Payload Ops Specification

Linalg provides a declarative specification and a generation tool (mlir-linalg-ods-gen) to automatically produce named ops from a notation that is inspired by Einstein notation.

The syntax and semantics used in mlir-linalg-ods-gen are very much in flight and borrow from Tensor Comprehensions (TC) but differ in a few dimensions, to better adapt to Linalg:

1. The input and output tensor parameters are specified as id : type(symbolic-affine-expression-list) (e.g. A : f32(M, N + M)) and each new symbol is discovered eagerly. TC on the other hand does not allow general symbolic affine expressions.
2. The output shapes are specified explicitly, in TC they are always derived from the input shapes.
3. The operations used to specify computations use EDSC intrinsics so that they can easily be parsed and emitted into a simple region builder without resorting to more general MLIR parsing.
4. Reduction dimensions are specified with angle bracket notation on the operation they apply to (e.g. std_add<k> specifies that k is a reduction dimension). In TC, a reduction is specified with op= operator and the reduction dimensions are inferred.
5. The parallel and reduction dimension are ordered by the textual program order. For instance, in the comprehension O(i, j) = std_add<k, l>(...), i (resp. j) is a parallel iterator encoded by affine dimension of position 0 (resp. 1); k (resp. l) is a reduction iterator encoded by an affine dimension of position 2 (resp. 3).

These decisions and syntax are subject to evolution and change. In particular, op-specific attributes, dynamic ranks, some form of templating, shape calculation function specification, etc. may be added in the future.

At this time, the following restrictions are imposed on the syntax and semantics:

1. Each def may only contain a single comprehension but each comprehension may perform multiple updates.
2. Each tensor may only be used with a single indexing expression.

The following specification may be used to define a named batchmatmul op:

def batchmatmul(A: f32(Batch, M, K), B: f32(K, N)) -> (C: f32(Batch, M, N)) {
  C(b, m, n) = std_addf<k>(std_mulf(A(b, m, k), B(k, n)));
}

When mlir-linalg-ods-gen -gen-ods-decl=1 is called, the following ODS is produced:

def batchmatmulOp : LinalgNamedStructured_Op<"batchmatmul", [
  NInputs<2>,
  NOutputs<1>,
  NamedStructuredOpTrait]> { ... }

When mlir-linalg-ods-gen -gen-impl=1 is called, the following C++ is produced:

llvm::Optional<SmallVector<StringRef, 8>> batchmatmul::referenceIterators() {
  return SmallVector<StringRef, 8>{
    getParallelIteratorTypeName(),
    getParallelIteratorTypeName(),
    getParallelIteratorTypeName(),
    getReductionIteratorTypeName() };
}
llvm::Optional<SmallVector<AffineMap, 8>> batchmatmul::referenceIndexingMaps() {
  MLIRContext *context = getContext();
  AffineExpr d0, d1, d2, d3;
  bindDims(context, d0, d1, d2, d3);
  return SmallVector<AffineMap, 8>{
      AffineMap::get(4, 0, {d0, d1, d3}),
      AffineMap::get(4, 0, {d3, d2}),
      AffineMap::get(4, 0, {d0, d1, d2}) };
}
void batchmatmul::regionBuilder(ArrayRef<BlockArgument> args) {
  using namespace edsc;
  using namespace intrinsics;
  Value _0(args[0]), _1(args[1]), _2(args[2]);
  Value _4 = std_mulf(_0, _1);
  Value _5 = std_addf(_2, _4);
  (linalg_yield(ValueRange{ _5 }));
}

Open Issues and Design Alternatives

Multiple open issues and design alternatives are in flight and it is time to lay them out for the community to discuss and pick apart:

1. Should linalg.generic support nesting?
2. Should linalg.generic regions take views or only scalars?
3. Should we try to solve automatic differentiation at this level of abstraction?
4. Are all the six properties really necessary?
5. Is this relying too much on declarative specification and would we be better off relying more on analyses?
6. Is this general enough for the community's needs? If not how should this be extended, if at all? ...

These key questions (and much more) should be really thought of in the general context of MLIR in which different levels of IR interoperate seamlessly. In practice, it is not necessary (or beneficial) to try and solve all problems in the same IR.

Operations

[include "Dialects/LinalgOps.md"]